This book is an introduction to the geometric theory used to design linkage systems that are critical components of machines ranging from vehicle suspensions to robot arms. The focus throughout is on graphical synthesis of linkages to control the movement of the legs for a walking machine.
Select this link to see the Kindle Interactive version in Amazon
Select to see this book in Apple Books
Select for the print version in Amazon.
Increasingly complicated walking machines obtained from patent drawings, art and technology are used to motivate the theory. Starting with legs formed by rotating cranks, we move to legs constructed from four bar linkages with specially shaped coupler curves. This leads to a search for coupler points that have near straight line trajectories, and motivates constructions for the inflection circle and cubic of stationary curvature. We also consider cognate linkages and those with symmetric coupler curves.
The use of an RR chain controlled by the coupler of a four-bar linkage is our introduction to six-bar linkages. Then skew pantographs that provide scaling and reorientation of a coupler curve for better walking movement yields eight-bar linkages. The legs designed by Theo Jensen and Amanda Gassaei are shown to implement four bar function generators that control the joint movement of an RR chain. This leads to graphical two and three position synthesis of four-bar function generators, which are applied to the design of legs with two and three specified configurations.
We end with a description of the duty factor and support pattern needed for two, four and six legged walking machines. The challenge of steering and suspension is left for the future.



 JMM
JMM JMM
JMM JMM
JMM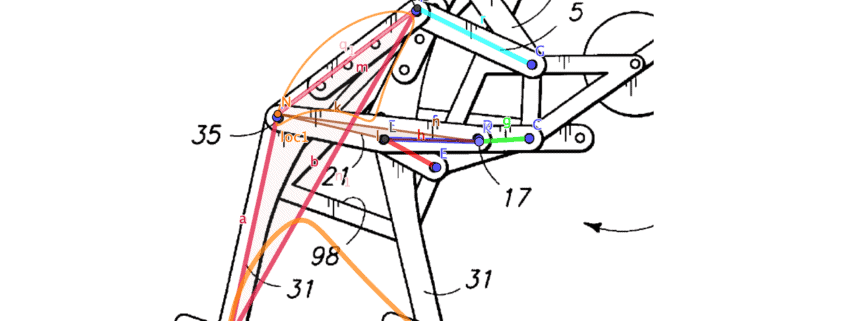 JMM
JMM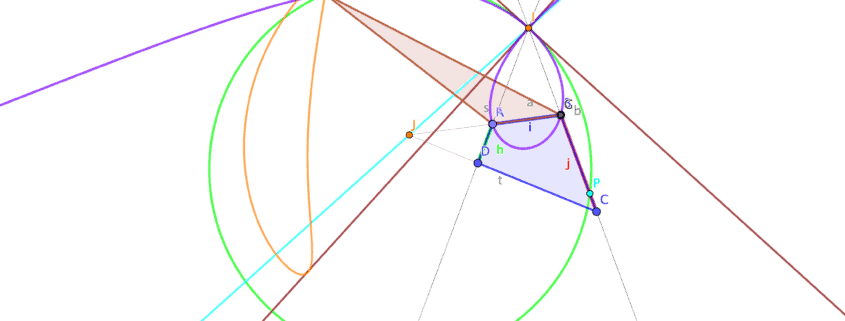 JMM
JMM JMM
JMM JMM
JMM JMM
JMM