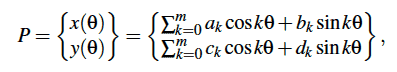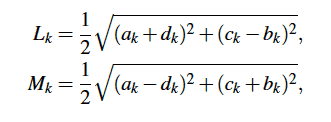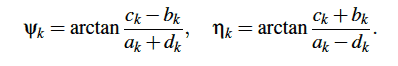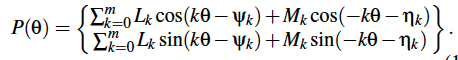Design of Drawing Mechanisms
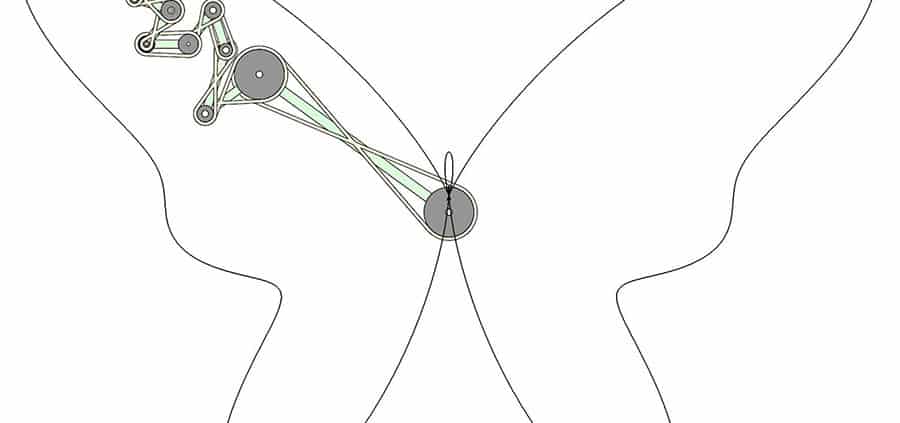
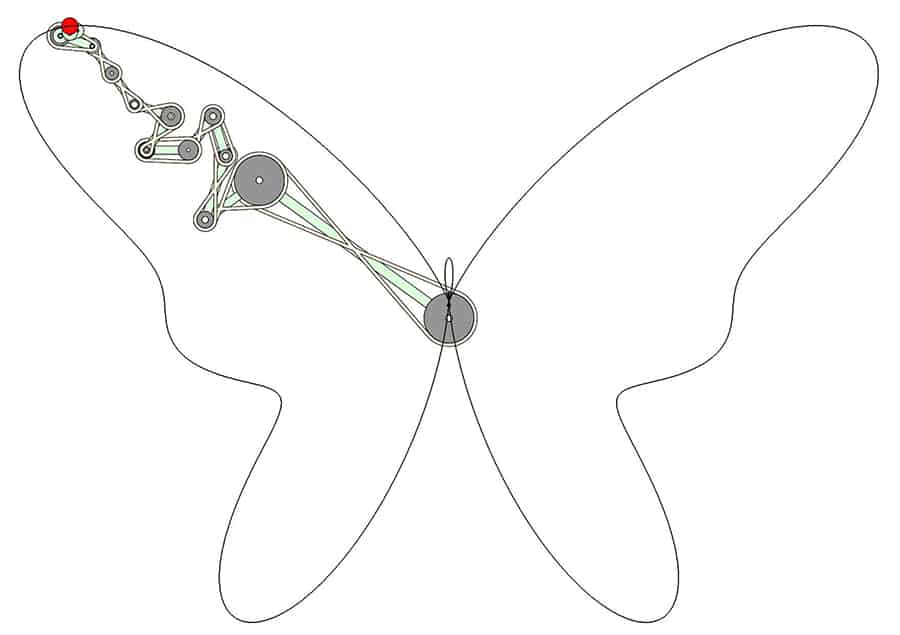
Mechanical systems that draw trigonometric curves provide a versatile way to draw complex curves. Yang Liu designed this serial chain consisting of 14 links coupled by a belt drive to draw the Butterfly curve.
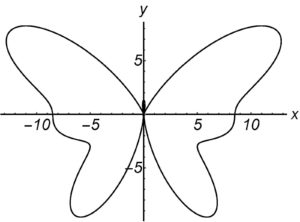
The Butterfly curve is an example of a trigonometric plane curve, and our study of Kempe’s design of linkages to draw algebraic curves has lead us to a way to design serial chains that draw these curves.
Here is how it is done.
Trigonometric curves. A trigonometric plane curve is a parametrized curve with coordinate functions, P = (x, y), that are finite Fourier series,
where ak , bk , ck and dk are real coefficients and theta ranges from 0 to $latex 2\pi$.
A large number of well-known curves have this form, such as Limacon of Pascal, the Cardioid, Trifolium, Hypocycloid and Lissajous figures.
A coupled serial chain. Without going into too much detail, it is possible to use the coefficients ak , bk, ck and dk to define the link dimensions,
and the initial angles,
These parameters allow us to redefine the trigonometric equations of the curve as the coordinate equations of the links of a serial chain,
This equation identifies the curve as the end of a serial chain consisting of a sequence of links L1, M1, L2, M2 and so on, such that the Lk links rotate counter clockwise and the Mk links rotate clockwise both at the rate $latex k\theta$.
The initial angles define the configuration of the serial chain when $latex \theta=0$.
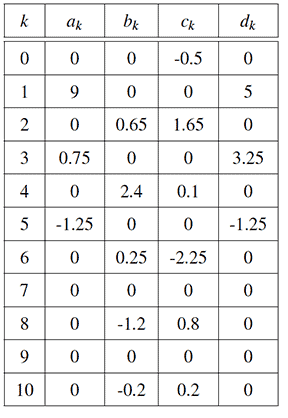
The Butterfly drawing mechanism. The trigonometric curve of the Butterfly linkage is defined by the coefficients in the following table,
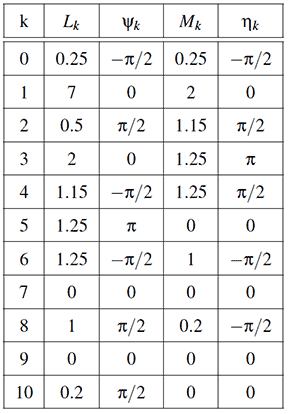
These coefficients are used to calculate the dimensions and initial configuration of the serial chain listed in the following table,
The result is a serial chain consisting of 14 links that are coordinated to move together as the base rotates. The end-point of the chain draws the Butterfly curve.