Want a patent? Try a Six-bar linkage
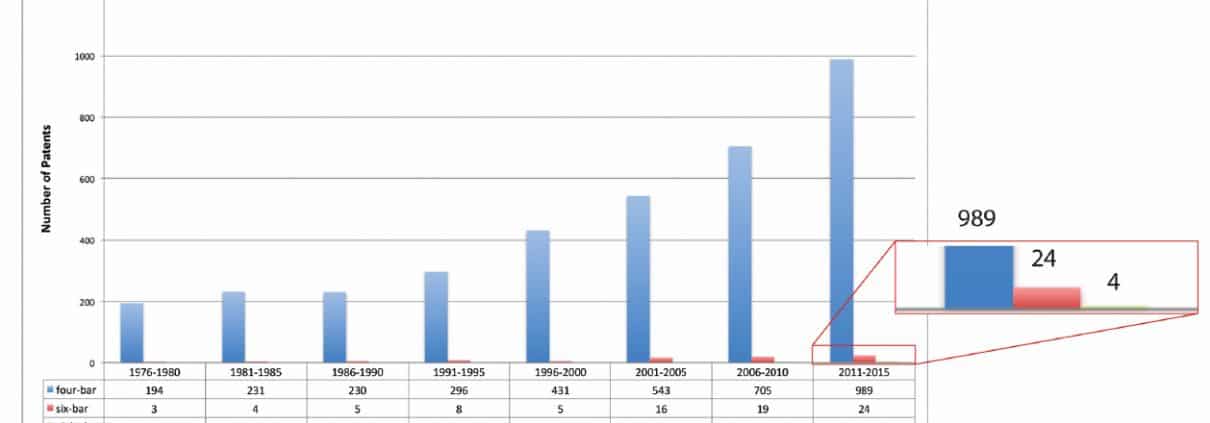
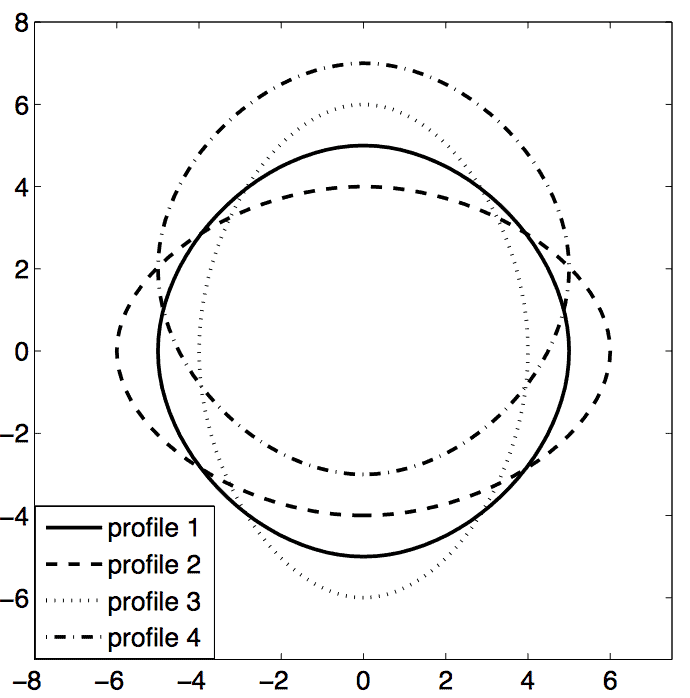
Patents including six-bar linkages are rare. Thousands of U.S. Patents have been awarded over the past forty years that involve four-bar linkages, but less than a hundred involve six-bar linkages, Figure 1.

Figure 1. Since 1976, 3619 patents have been awarded that involve four-bar linkages and only 84 that involve six-bar linkages.
Add two bars to a four-bar to get a six-bar. A four-bar linkage, familiar to all mechanical designers, has an input lever connected by a rod to an output lever, Figure 2 (top). Add two more bars and you have a six-bar linkage. Unfortunately, the standard way to add those bars yields sequence of two four-bar linkages, Figure 2 (bottom), which is not really new. There are other ways to add these two bars but they are beyond the state-of-the-art.

Figure 2. Add two bars to a four-bar linkage (top) to obtain a sequence of two four-bar linkages (bottom). This is the best designers can currently do for a six-bar linkage.
Other ways to add two bars. The two additional bars can be added to a four-bar linkage by attaching one end to the connecting rod and the other end to the output link. The result is a stack of two four-bar linkages, known as the Watt I six-bar linkage, Figure 3(a).
Another way is to connect one end of the two bars to the input lever and the other to output lever. This can be done in two ways, either on top of or beneath the four-bar linkage. When added on top, the result is a five-bar loop stacked on the four-bar linkage, known as the Stephenson I six-bar, Figure 3(b). When added beneath, the four-bar linkage is stacked on a five-bar loop, which is a Stephenson II sixbar, Figure 3 (c).
A systematic procedure for design of these alternative six-bar linkages is simply not available to mechanical designers.
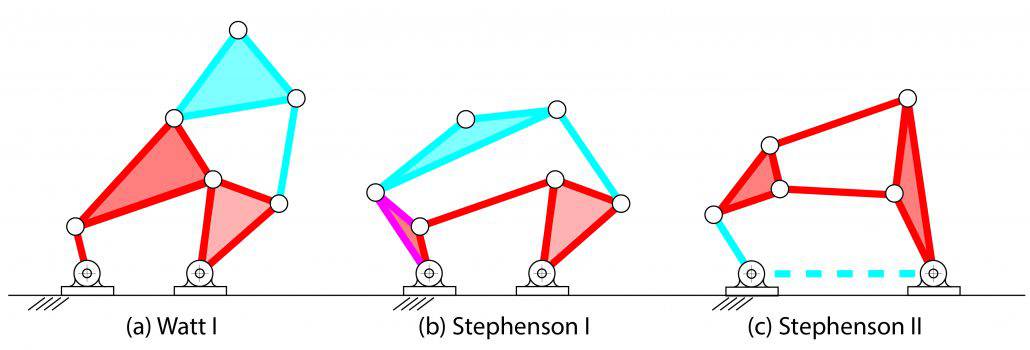
Figure 3. Three ways to add two bars to a four-bar linkage to obtain a six-bar linkage, each of which is beyond the state-of-the-art.
Solving the loop equations for four-bar and six-bar linkages. There is a simple, though mathematical, reason why four-bar linkages are easy to design and six-bar linkages that are more than a sequence of two four-bar linkages are very hard to design.
Almost sixty years ago in 1954, Ferdinand Freudenstein showed that if we define the movement required of a four-bar linkage, then its dimensions can be computed from its loop equations, which in modern form are give by,

Four-bar Loop Equations
He also showed that the solution of these equations is equivalent to finding the roots of a fourth degree polynomial, which is easy to do.
Soon afterward researchers obtained two sets of loop equations for six-bar linkages and showed that for a required movement, the solution of its loop equations,

Six-bar Loop Equations
is equivalent to finding the roots of a polynomial system of degree, d=264×10^6. A complete solution was only recently achieved after 300 hours of computation on a high performance computer cluster.
This stunning increase in complexity gets worse for eight-bar linkages obtained by adding two bars to a six-bar linkage, which yields three sets of loop equations. In this case calculating the dimensions of the linkage involves the solution of a polynomial system estimated to be of degree, d=10^15, which is massively beyond capabilities of even theoretical polynomial solvers.
A four-bar with additional design parameters. Once we understand the structure of the design equations for four-bar, six-bar and even eight-bar linkages, it is possible to take a different approach to the problem of calculating a design from a movement requirement.
A four-bar linkage has eight design variables, which are the four pairs of coordinates that define its hinged joints. Similarly, a six-bar linkage has seven hinged joints or 14 design parameters, and an eight-bar linkage has 10 joints or 20 design parameters. It is possible to consider a six-bar and even an eight-bar linkage as a four-bar linkage with extra design variables. The question then becomes how to use these extra design variables to improve the performance of the linkage system.
Six-bar linkages provide simple and effective movement. But is there ever a situation where the complexity of a six-bar linkage is preferred over a four-bar linkage that provides the same movement? Of course there is, but let’s let design engineers describe their experience.
Søren Matthesen, design engineer for Vendlet Aps, which makes automated equipment for beds, studied the use of gears, guide rails and four-bar linkages and wound up using a six-bar linkage for his application. He states,
“What really mattered to me was the fact that the six-bar linkage enabled me to solve my design task unlike the four-bar linkage. This is a huge advantage in functionality. Compared to my initial solutions, the six-bar linkage system ends up being more simple and stable to produce, use and maintain.”
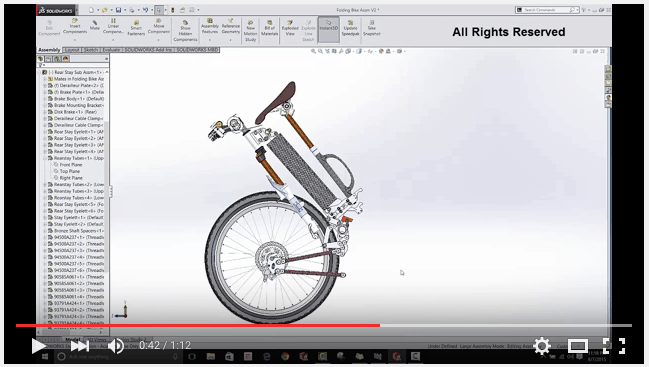
Mike Sutherland, design engineer, Zennen Engineering, designed a six-bar linkage to fold the rear wheel of a new full-scale folding bicycle, Figure 4. He states,
“The six-bar rearstay folding linkage provided very tight package; that besides being convenient for transportation, also has something of a ‘Transformer’ attraction about it…”

Figure 4. The Zennen folding bicycle concept uses a six-bar linkage to fold the full-sized rear wheel against the folded front forks, downtube and seat tube.
The simple answer is that a six-bar linkage designed to achieve the same movement as a four-bar linkage will have free design parameters that allow optimization of other features important to the designer, and this definitely justifies the increase in complexity. And it may be an invention ready for a U. S. Patent.